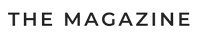אַדאַפּטיישאַנז דעוועלאָפּעד דורך וויקטימס צו טאָמבאַנק פּרעדאַטערז ביישטייערן צו דער אַנטוויקלונג פון מעקאַניזאַמז פֿאַר פּרעדאַטערז צו באַקומען די אַדאַפּטיישאַנז. די לאַנג קאָויגזיסטאַנס פון פּרעדאַטערז און וויקטימס פירט צו די פאָרמירונג פון אַ סיסטעם פון ינטעראַקשאַן אין וואָס ביידע גרופּעס זענען סטאַבלי אפגעהיט אין די לערנען געגנט. ווייאַליישאַן פון אַזאַ אַ סיסטעם אָפט פירן צו נעגאַטיוו ינווייראַנמענאַל פאלגן.

די נעגאַטיוו פּראַל פון די הילעל פון קאָו-עוואָולושאַנערי באַציונגען איז באמערקט בעשאַס די הקדמה פון מינים. אין באַזונדער, גאָוץ און ראַבאַץ ינטראָודוסט אין אַוסטראַליאַ טאָן ניט האָבן עפעקטיוו שפע מעקאַניזאַמז אויף דעם קאָנטינענט, וואָס פירט צו די צעשטערונג פון נאַטירלעך יקאָוסיסטאַמז.

מאַטאַמאַטיקאַל מאָדעל

רעכן אַז צוויי מינים פון אַנימאַלס באַוווינען אַ זיכער טעריטאָריע: ראַבאַץ (פידינג אויף געוויקסן) און פאָקסעס (פידינג אויף ראַבאַץ). לאָזן די נומער פון ראַבאַץ x < displaystyle x>, די נומער פון פאָקסעס y < displaystyle y>. ניצן די Malthus מאָדעל מיט די נייטיק אַמענדמאַנץ, גענומען אין חשבון די עסן פון ראַבאַץ דורך פאָקסעס, מיר קומען צו די פאלגענדע סיסטעם מיט די נאָמען פון די Volterra מאָדעל - טאַץ:

<x ˙ = (α - c y) x, y ˙ = (- β + d x) y. < displaystyle < אָנהייבן< פּונקט > = ( alpha -cy) x, < dot > = (- beta + דקס) וויי. סוף>>

דער סיסטעם האט אַ יקוואַליבריאַם שטאַט ווען די נומער פון ראַבאַץ און פאָקסעס איז קעסיידערדיק. דיווייישאַן פון דעם שטאַט פירט צו פלאַקטשויישאַנז אין די נומער פון ראַבאַץ און פאָקסעס, ענלעך צו פלאַקטשויישאַנז אין די האַרמאָניק אַסאַלייטער. ווי אין דעם פאַל פון אַ האַרמאָניק אַסאַלייטער, די נאַטור איז נישט סטראַקטשעראַלי סטאַביל: אַ קליין ענדערונג אין דעם מאָדעל (למשל, אויב איר נעמען אין חשבון די לימיטעד רעסורסן וואָס ראַבאַץ דאַרפֿן), קען פירן צו אַ קוואַליטאַטיווע ענדערונג אין נאַטור. למשל, אַ יקוואַליבריאַם שטאַט קענען ווערן סטאַביל, און פלאַקטשויישאַנז אין נומערן וועט פאַרפוילן. דער פאַרקערט סיטואַציע איז אויך מעגלעך, ווען קיין קליין דיווייישאַן פון די יקוואַליבריאַם שטעלע וועט פירן צו קאַטאַסטראָפיק קאַנסאַקווענסאַז, ביז אַ גאַנץ יקסטינגשאַן פון איינער פון די מינים. ווען געפרעגט וועגן וואָס פון די סינעריאָוז זענען ימפּלאַמענאַד, די Volterra-טרייַ מאָדעל קען נישט געבן אַן ענטפער: נאָך פאָרשונג איז פארלאנגט דאָ.

פֿון דער מיינונג פון די טעאָריע פון ​​אַסאַליישאַנז, די Volterra - Lotka מאָדעל איז אַ קאָנסערוואַטיווע סיסטעם מיט דער ערשטער ינטעגאַל פון באַוועגונג. די סיסטעם איז נישט גראָב ווייַל די מינדסטע ענדערונגען אין די רעכט זייַט פון די יקווייזשאַנז פירן צו קוואַליטאַטיווע ענדערונגען אין דינאַמיש נאַטור. אָבער, עס איז מעגלעך צו "אַ ביסל" מאָדיפיצירן די רעכט זייַט פון די יקווייזשאַנז אַזוי אַז די סיסטעם ווערט זיך-אַסאַלייטינג. די בייַזייַן פון אַ סטאַביל לימאַץ ציקל טאָכיק אין פּראָסט דינאַמיש סיסטעמען קאַנטריביוץ צו אַ באַטייַטיק יקספּאַנשאַן פון די פעלד אַפּלאַקאַבילאַטי פון די מאָדעל.

מאָדעל נאַטור

די גרופּע לייפסטייל פון פּרעדאַטערז און זייער וויקטימס ראַדיקאַללי ענדערונגען די נאַטור פון די מאָדעל, און דאָס ינקריסיז די פעסטקייַט.

סייכל: מיט אַ גרופּע לייפסטייל דיקריסאַז די אָפטקייַט פון טראַפ - ינקאַונטערז פון פּרעדאַטערז מיט פּאָטענציעל וויקטימס, וואָס איז באשטעטיקט דורך אַבזערוויישאַנז פון די דינאַמיק נומער פון ליאָנס און ווילדעבעעסץ אין סערענגעטי פארק.

געשיכטע

דער מאָדעל פון דער קאָויגזיסטאַנס פון צוויי בייאַלאַדזשיקאַל מינים (פּאַפּיאַליישאַנז) פון די "פּרעדאַטער - רויב" טיפּ איז אויך גערופן די וואָלטעראַ - לאָטקאַ מאָדעל.

Alfred Lotka איז געווען ערשטער דערגרייכט אין 1925 (געוויינט צו שילדערן די דינאַמיק פון ינטעראַקטינג בייאַלאַדזשיקאַל פּאַפּיאַליישאַנז).

אין 1926 (ראַגאַרדלאַס פון Lotka) זענען ענלעך (און מער קאָמפּליצירט) מאָדעלס דעוועלאָפּעד דורך דער איטאַליעניש מאַטאַמאַטישאַן Vito Volterra. זיין טיף שטודיום אין די פעלד פון ינווייראַנמענאַל פּראָבלעמס געלייגט דעם יסוד פֿאַר די מאַטאַמאַטיקאַל טעאָריע פון ​​בייאַלאַדזשיקאַל קהילות (מאַטאַמאַטיקאַל יקאַלאַדזשי).